혼자 공부하는 머신러닝+딥러닝 - 예스24
- 혼자 해도 충분하다! 1:1 과외하듯 배우는 인공지능 자습서 이 책은 수식과 이론으로 중무장한 머신러닝, 딥러닝 책에 지친 ‘독학하는 입문자’가 ‘꼭 필요한 내용을 제대로’ 학습할 수 있
www.yes24.com
비지도 학습(Unsupervised Learning)
비지도 학습은(Unsupervised Learning) 학습 알고리즘의 결과물이라고 할 수 있는 출력(target)을 미리 제공하지 않고 인공지능(AI)이 입력 데이터에서 패턴과 상관관계를 찾아내야 하는 머신러닝 알고리즘이다.
과일 사진 데이터를 분류하는 연습을 해 보겠다.
import numpy as np
import matplotlib.pyplot as plt
!wget https://bit.ly/fruits_300_data -0 fruits_300.npy # 리눅스 명령어를 이용해 데이터 다운로드
fruits = np.load('fruits_300npy') # 파일 불러오기
print(fruits.shape)
# output
# (300, 100, 100)
fruits는 3차원(300, 100, 100)의 numpy 배열이고 첫 번째 차원은 이미지 수, 두 번째 차원은 이미지 높이(height), 세 번째 차원(100) 이미지의 가로(width)를 의미한다.

첫 번째 이미지의 첫 번째 행을 출력해 보면 다음과 같다.
print(fruits[0, 0, :])
# output
# [ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1
# 2 2 2 2 2 2 1 1 1 1 1 1 1 1 2 3 2 1
# 2 1 1 1 1 2 1 3 2 1 3 1 4 1 2 5 5 5
# 19 148 192 117 28 1 1 2 1 4 1 1 3 1 1 1 1 1
# 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
# 1 1 1 1 1 1 1 1 1 1]
이 배열을 이용해서 어떤 이미지인지 확인해 본다. numpy 배열의 이미지는 imshow() 함수를 사용한다.
plt.figure(figsize = (4, 3))
plt.imshow(fruits[0], cmap = 'gray')
plt.figure(figsize = (8, 6))
for i in range(3):
ax = plt.subplot(1, 3, i + 1)
ax.imshow(fruits[i * 100], cmap = 'gray_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
- 픽셀 값 분석하기
fruits 데이터를 분석하기 위해 전체 데이터를 과일 종류별로 나눈다. 이는 numpy 배열로 처리하기 용이하기 때문이다.

apple = fruits[0:100].reshape(-1, 100 * 100)
pineapple = fruits[100:200].reshape(-1, 100 * 100)
banana = fruits[200:300].reshape(-1, 100 * 100)
print(apple.shape)
# output
# (100, 10000)
샘플 데이터를 이용해 픽셀의 평균값을 구해서 이미지를 예측할 수 있는지 확인해 보겠다.

print(apple.mean(axis = 1)) # axis = 1, 샘플별 픽셀의 평균
# array([ 88.3346, 97.9249, 87.3709, 98.3703, 92.8705, 82.6439,
# 94.4244, 95.5999, 90.681 , 81.6226, 87.0578, 95.0745,
# 93.8416, 87.017 , 97.5078, 87.2019, 88.9827, 100.9158,
# 92.7823, 100.9184, 104.9854, 88.674 , 99.5643, 97.2495,
# 94.1179, 92.1935, 95.1671, 93.3322, 102.8967, 94.6695,
# 90.5285, 89.0744, 97.7641, 97.2938, 100.7564, 90.5236,
# 100.2542, 85.8452, 96.4615, 97.1492, 90.711 , 102.3193,
# 87.1629, 89.8751, 86.7327, 86.3991, 95.2865, 89.1709,
# 96.8163, 91.6604, 96.1065, 99.6829, 94.9718, 87.4812,
# 89.2596, 89.5268, 93.799 , 97.3983, 87.151 , 97.825 ,
# 103.22 , 94.4239, 83.6657, 83.5159, 102.8453, 87.0379,
# 91.2742, 100.4848, 93.8388, 90.8568, 97.4616, 97.5022,
# 82.446 , 87.1789, 96.9206, 90.3135, 90.565 , 97.6538,
# 98.0919, 93.6252, 87.3867, 84.7073, 89.1135, 86.7646,
# 88.7301, 86.643 , 96.7323, 97.2604, 81.9424, 87.1687,
# 97.2066, 83.4712, 95.9781, 91.8096, 98.4086, 100.7823,
# 101.556 , 100.7027, 91.6098, 88.8976])
plt.hist(np.mean(apple, axis = 1), alpha = 0.8)
plt.hist(np.mean(pineapple, axis = 1), alpha = 0.8)
plt.hist(np.mean(banana, axis = 1), alpha = 0.8)
plt.legend(['apple', 'pineapple', 'banana'])
파인애플과 바나나도 평균을 구하고 그 결과를 히스토그램으로 나타낸다.

바나나는 비교적 잘 구분이 되지만 사과와 파인애플은 구분이 어렵다. 이번에는 픽셀별 평균값을 구해보자.
fruit = [apple, pineapple, banana]
plt.figure(figsize = (12, 4))
for i in range(3):
ax = plt.subplot(1, 3, i + 1)
plt.bar(range(10000), np.mean(fruit[i], axis = 0), alpha = 0.8)
plt.legend(['apple', 'pineapple', 'banana'])
plt.tight_layout()
plt.show()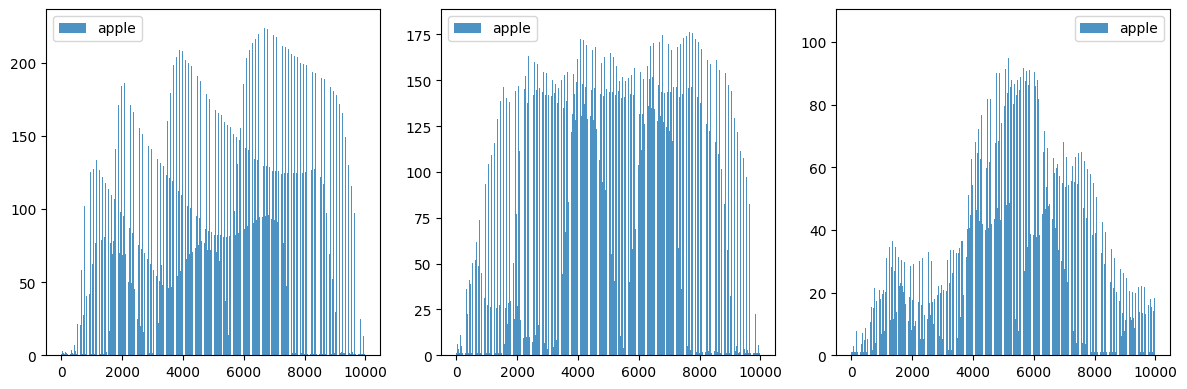
이렇게 구한 픽셀별 평균값을 100 X 100 크기로 바꿔서 이미지처럼 출력하여 그래프와 비교해 본다. 이는 과일벼로 모든 사진을 모아 놓은 대표 이미지로 생각할 수 있다.
apple_mean = np.mean(apple, axis = 0).reshape(100, 100)
pineapple_mean = np.mean(pineapple, axis = 0).reshape(100, 100)
banana_mean = np.mean(banana, axis = 0).reshape(100, 100)
fruit_mean = [apple_mean , pineapple_mean , banana_mean ]
plt.figure(figsize = (4, 3))
for i in range(3):
ax = plt.subplot(1, 3, i + 1)
ax.imshow(fruit_mean[i], cmap = 'gray_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.tight_layout()
plt.show()
사과 사진의 평균값이 apple_mean을 이용해 사과 사진만 선택해 보자. 절댓값 오차를 이용해 fruits 배열에 있는 모든 샘플에서 apple_mean을 뺀 절댓값의 평균을 구하면 될 것이다. 그 결과는 크기가 (300,)인 1차원 배열이다. 평균을 구할 때 (300, 100, 100)에서 300은 이미지 숫자를 나타내기 때문에 평균 계산에 포함하지 않는다. 두 번째, 세 번째 차원에 대해서 평균을 구할 것이기 때문에 axis = (1, 2)를 사용한다.
abs_diff = np.abs(fruits - apple_mean)
abs_mean = np.mean(abs_diff, axis = (1, 2))
print(abs_mean[:100])
# output
# [17.37576 13.508874 17.183394 15.68311 17.983306 20.565392 16.795812
# 16.144276 19.611994 21.32059 16.454222 16.590134 13.37039 17.23263
# 15.92806 15.496638 18.582212 16.48196 27.651556 19.7871 20.826912
# 16.417934 17.059946 15.904296 15.086176 19.371364 24.076362 14.777732
# 19.20517 20.805182 14.797906 18.658418 15.973216 13.04259 18.381052
# 16.59904 16.288504 18.960586 13.88574 16.497594 18.40376 19.174642
# 29.096702 18.40849 28.223962 21.42994 19.740466 15.590532 13.082678
# 18.765996 14.391198 21.464746 26.261028 15.887148 18.568706 16.410426
# 17.108034 13.178824 18.199846 13.503056 20.845032 16.898184 22.81774
# 18.99896 19.102706 16.636216 14.845644 19.357872 14.778086 14.468082
# 13.085526 15.946606 20.42774 16.241996 13.720382 18.416166 15.229106
# 16.411342 13.47148 20.050622 17.296816 21.071312 18.451708 19.645494
# 15.585712 20.582004 13.850318 13.269222 21.875262 17.152098 15.60477
# 23.890138 14.442124 18.794826 15.750524 16.58135 19.375552 17.802096
# 15.478418 16.542458]
apple_mean과 오차가 작은 샘플 100개를 확인하고 300개의 평균 값을 오름차순으로 100개를 골라보자. numpy 함수 중 argsort() 함수를 사용한다.이렇게 하면 픽셀별 평균값이 사과를 예측할 때 유용한지 확인해 볼 수 있다.
apple_index = np.argsort(abs_mean)[:100]
plt.figure(figsize = (5, 5))
for i in range(100):
ax = plt.subplot(10, 10, i + 1)
ax.imshow(fruits[apple_index[i]], cmap = 'gray_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.tight_layout()
plt.show()
이렇게 비슷한 샘플끼리 모으는 작업을 군집(clustering)이라고 하며 대표적인 비지도 학습에 해당한다. 군집 알고리즘에서 대표적인 것이 K-Means Clustering이며 군집 알고리즘이 만든 그룹을 cluster라고 한다.
K - Means Clustering
- 분류(Clustering)
지금까지의 예시와 달리 비지도 학습인 분류는 target을 알지 못하는 상태에서 수행하게 된다. 따라서 특성에 따라 클러스로 분류해주는 K - 평균 알고리즘을 사용한다면 문제 해결에 도움이 될 것이다. K - 평균 알고리즘은 다음과 같이 작동한다.
- 무작위로 k 개의 클러스터 중심을 정한다.
- 각 샘프에서 가장 가까운 클러스터 중심을 찾아 해당 클러스터의 샘플로 지정한다.
- 클러스터에 속한 샘플의 평균값으로 크러스터 중심을 변경한다.
- 크러스터 중심에 변화가 없을 때까지 2번으로 돌아가 반복한다.
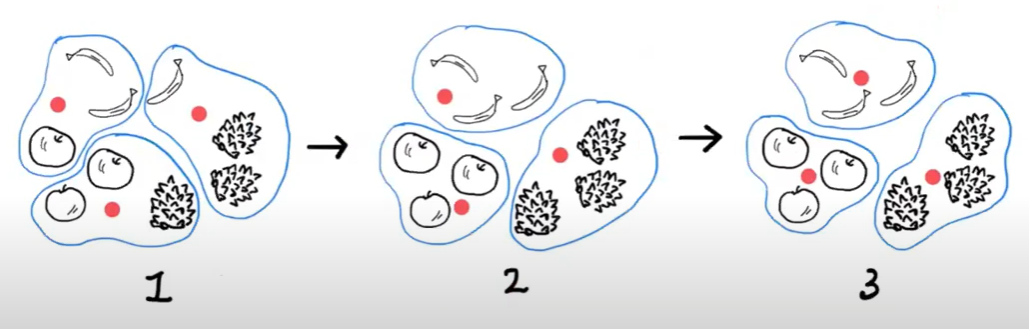
사이킷런에는 sklearn.cluster 모듈 아래 KMeans 클래스에 구현되어 있다. 이 클래스에서 설정할 매개변수는 클러스터의 개수인 n_clusters이다.
from sklearn.cluster import KMeans
fruits_2d = fruits.reshape(-1, 100 * 100)
km = KMeans(n_clusters = 3, random_state = 42)
km.fit(fruits_2d)
print(np.unique(km.labels_, return_counts = True))
# output
# (array([0, 1, 2], dtype=int32), array([111, 98, 91]))
군집된 결과는 KMeans 클래스 객체의 labels_ 속성에 저장되어 있다. labels_ 배열의 길이는 샘플 개수와 같다. n_clusters = 3이기 때문에 이 배열의 값은 0, 1, 2 중 하나일 것이다. 그리고 0, 1, 2는 실제 어느 과일을 의미하는지도 알 수 없다.
각 클러스터가 어떤 이미지를 나타내는지 알아보기 위해 그림을 출력하기 위한 함수를 정의해 보자,
def draw_fruits(arr, ratio = 0.5):
n = len(arr) # 입력된 이미지의 수
rows = int(np.ceil(n / 10)) # np.ceil은 올림 처리를 하는데 실수를 반환, int로 정수 처리
cols = n if rows < 2 else 10
plt.figure(figsize = (cols * ratio, rows * ratio))
for i in range(n):
ax = plt.subplot(rows, cols, i + 1)
ax.imshow(arr[i], cmap = 'gray_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.tight_layout()
plt.show()
draw_fruits(fruits[km.labels_ == 2]) # 전체 과일 이미지 중에 labels_가 2인 데이터만 boolean indexing 한다.
draw_fruits(fruits[km.labels_ == 1])

- 클러스터 중심(Centroid)
KMeans 클래스가 최종적으로 찾은 클러스터 중심은 cluster_centers_ 속성에 저장되어 있다. 이 배열은 fruits_2d(샘플 개수, 높이 X 너비) 샘플의 클러스터 중심이기 때문에 각 중심을 이미지로 출력하려면 100 X 100 크기의 2차원 배열로 바꿔야 한다. 이렇게 하면 크러스터 중심의 이미지를 볼 수 있다.
draw_fruits(km.cluster_centers_.reshape(-1, 100, 100), ratio = 1)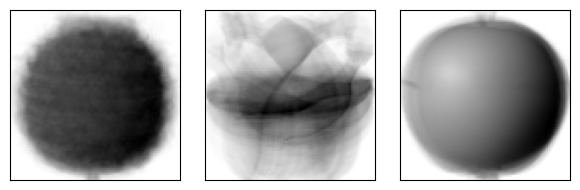
KMeans 클래스는 샘플 데이터에서 클러스터 중심까지의 거리를 구해주는 transfromt() 메서드를 가지고 있다. index가 100인 샘플에 대해 거리를 구해보자. 현재 2차원 배열인 fruits_2d를 이용해 학습한 상태라는 점을 잊지 말자.
km.transform(fruits_2d[100:101]) # 하나의 값을 indexing 하더라도 슬라이싱을 적용하면 2차원 배열을 반환받을 수 있다.
# output
# array([[3393.8136117 , 8837.37750892, 5267.70439881]])
첫 번째 값은 labels_ = 0 인 centroid와의 거리, 두 번째 값은 labels_ = 1 인 centroid와의 거리이다. 이 샘플은 labels_가 0인 과일에 해당될 것이다.
draw_fruits(fruits[100:101], ratio = 2)
예측을 출력해주는 predict() 메서드를 사용할 수도 있다.
km.predict(fruits_2d[100:101])
# output
# array([0], dtype=int32)
K - Means 알고리즘이 몇 번의 클러스터 중심 이도을 통해 학습했는지를 알려주는 n_iter_ 속성도 있다.
- 최고의 K 찾기
K - Means 알고리즘의 단점 중 하나는 크러스터 개수를 사전에 지정해야 한다는 점이다. 몇 개의 클러스터가 있는지 알 수 없기 때문인데 어떻게 하면 적절한 K를 찾을 수 있는지 알아보겠다.
엘보우(elbow) 방법
K - Means 알고리즘은 클러스터 중심과 클러스터에 속한 샘플 사이의 거리를 재는 것이다. 이 거리의 제곱 합을 이너셔(inertia)라고 한다. 이너셔는 클러스터에 속한 샘플이 얼마나 가깝게 모여 있는지를 나타내는 값이라고 생각할 수 있다. 일반적으로 클러스터의 수가 늘어나면 클러스터 개개의 크기가 줄어들기 때문에 이너셔도 작아지게 된다. 엘보우 방법은 크러스터 개수를 늘려가면서 이너셔의 변화를 관찰하여 최적의 클러스터 개수를 찾는 것이다.
fruits 데이터를 이용해 실습해 보겠다.
inertia = []
for k in range(2, 7):
km = KMeans(n_clusters = k, random_state = 42)
km.fit(fruits_2d)
inertia.append(km.inertia_)
plt.plot(range(2, 7), inertia)
plt.xlabel('k')
plt.ylabel('inertia')
plt.show()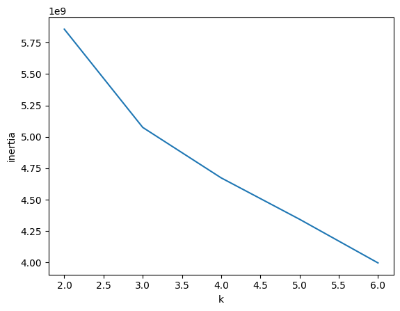
주성분 분석(Principal Compressed Analysis)
선형 회귀에서 본 것 처럼 특성이 많으면 모델의 성능이 높아지고 훈련 데이터에 과적합된다. 차원 축소는 데이터를 가장 잘 나타내는 일부 특성을 선택하여 데이트 크기를 줄이고 지도 학습 모델의 성능을 향상시킬 수 있는 방법이다. 줄어든 차원에서 다시 원본 차원으로 손실을 최대한 줄이면서 복원할 수도 있다.대표적인 차원 축소 알고리즘에는 주성분 분석(PCA)이 있다.
PCA는 데이터에 있는 분산이 큰 방향을 찾는 것이라고 할 수 있다. 분산은 데이터가 널리 퍼져있는 정도를 말한다. 분산이 큰 방향이란 데이터를 잘 표현하는 어떤 벡터라고 생각할 수 있다.
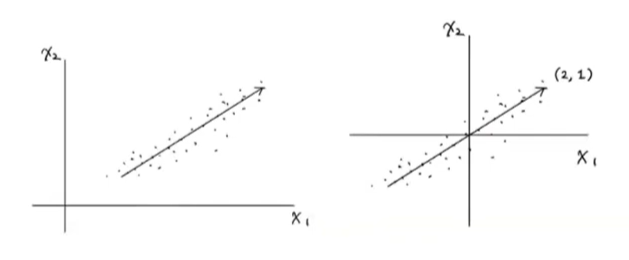
위에서 데이터는 x1, x2의 2개 특성이 있다. 분산이 가장 큰 방향은 데이터의 분포를 가장 잘 표현하는 방향이므로 오른쪽 위로 길게 늘어선 대각선 방향이 분산이 가장 크다고 할 수 있다. 화살표의 위치는 큰 의미가 없다는 점에 주의하자. 중요한 것은 분산이 큰 방향을 찾는 것이다. 위 그래프에서 직선이 원점을 지난다면 두 원소로 이루어진 벡터로 쓸 수 있다. 여기서는 (2, 1)이다. 이 벡터를 주성분(princi;al component)이라고 한다.
이 주성분 벡터에서 원소 개수는 원본 데이터에 있는 특성 개수와 같다. 원본 데이터는 주성분을 사용해 차원을 줄일 수 있다. (4, 2)를 주성분에 수직으로 투영하면 (4.5)이므로 차원이 감소하게 된다. 주성분이 가장 부난이 큰 방향이기 때문에 주성분에 투영하여 바꾼 데이터는 원본이 가지고 있는 특성을 가장 잘 나타낸다고 할 수 있을 것이다.
PCA 클래스
사이킷런은 sklearn.decomposition 모듈 아래 PCA 클래스로 주성분 분석 알고리즘을 제공한다. PCA 클래스의 객체를 만들 때 n_components 매개변수에 주성분의 개수를 지정해야 한다. K - Means 알고리즘과 마찬가지로 비지도 학습이기 때문에 fit() 메서드에 target을 제공하지 않는다.
from sklearn.decomposition import PCA
pca = PCA(n_components = 50)
pca.fit(fruits_2d)
print(pca.components_.shape)
print(pca.components_)
# output
# (50, 10000) # 사용자가 지정한 50, 원본 데이터의 특성 개수 10,000
# array([[ 9.24490195e-06, 5.10601298e-06, 8.91640398e-06, ...,
# 0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
# [-1.69701617e-05, -1.13551047e-05, -1.82152563e-05, ...,
# -0.00000000e+00, -0.00000000e+00, -0.00000000e+00],
# [-3.65220473e-05, -2.08401717e-05, -2.89870110e-05, ...,
# 0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
# ...,
# [-1.02766861e-05, -8.74813529e-05, -5.69534084e-05, ...,
# -0.00000000e+00, -0.00000000e+00, -0.00000000e+00],
# [-9.42699030e-05, -4.97956789e-05, -9.56824348e-05, ...,
# 0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
# [ 1.38991002e-04, -9.63198801e-05, -5.13484631e-05, ...,
# 0.00000000e+00, 0.00000000e+00, 0.00000000e+00]])
(50, 10000)에서 모델이 찾은 주성분은 50개이고 각 주성분은 요소의 수가 10,000인 벡터이다. 따라서 각 요소는 원본 픽셀에 가중치가 부여된 픽셀의 역할을 한다고 할 수 있다. 주성분을 reshape() 함수를통해 100 X 100 크기의 변환하면 이미지를 출력할 수 있다.
draw_fruits(pca.components_.reshape(-1, 100, 100))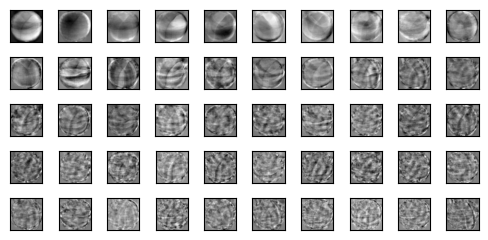
이 주성분은 원본 데이터에서 가장 분산이 큰 방향을 순서대로 나타낸 것이다. 한편으로는 데이터에 있는 어떤 특징을 잡아낸 것으로 생각할 수도 있다.
주성분을 찾았다면 원본 데이터를 주성분에 투영하여 특성의 개수를 줄일 수 있다. 마치 워본 데이터를 각 주성분으로 분해한다고 생각할 수 있다. PCA의 transform() 메서드를 이용해 원본 데이터의 차원을 줄일 수 있다.
print(fruits_2d.shape)
# output
# (300, 10000)
fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape)
# output
# (300, 50)
이렇게 하면 10,000개의 특성이(픽셀 하나를 특성이라고 볼 수 있기 때문에) 50개로 줄었다. 이로 인해 정보의 손실이 발생할 수 밖에 없지만 최대한 분산이 큰 방향으로 데이터를 투영했기 때문에 원본 데이터를 상당 부분 재구성할 수 있다. PCA는 이를 위해 inverse_transform() 메서드를 제공한다.
fruits_inverse = pca.inverse_transform(fruits_pca)
print(fruits_inverse.shape)
# output
# (300, 10000)
이 데이터를 100 X 100으로 바꾸어 이미지를 출력해 보자.
fruits_reconstruct = fruits_inverse.reshape(-1, 100, 100)
for start in [0, 100, 200]:
draw_fruits(fruits_reconstruct[start:start + 100])
print('\n')

- 설명된 분산(Explained Variance)
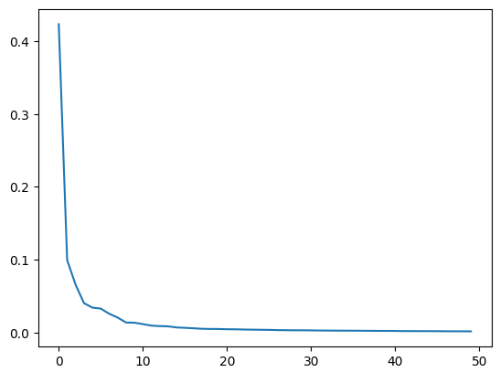
주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값을 설명된 분산이라고 한다. PCA 클래스의 explained_variance_ratio_에 각 주성분의 설명된 분산 비율이 기록되어 있다. 이 분산 비율을 모두 더하면 모든 주성분이 표현하고 있는 총 분산 비율을 구할 수 있다. 또한 plot() 함수로 설명된 분산의 비율을 그래프로 그릴 수 있다.
np.sum(pca.explained_variance_ratio_) # 50개의 특성이 92% 이상의 분산을 유지하고 있다.
# output
# 0.9214517417030338
plt.plot(pca.explained_variance_ratio_)
다른 알고리즘과 함께 사용하기
다음은 로지스틱 회귀 모델에 PCA를 적용하는 내용이다.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_validate
lr = LogisticRegression()
target = np.array([0] * 100 + [1] * 100 + [2] * 100)
scores = cross_validate(lr, fruits_2d, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
scores_pca = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
# output
# 0.9966666666666667
# 2.1550753593444822
# 0.9966666666666667
# 2.1550753593444822
PCA 클래스에 n_components 매개변수에 주성분의 개수를 지정하는 대신 설명된 분산의 비율을 입력할 수도 있다. PCA 클래스는 지정된 비율에 도달할 때까지 자동으로 주성분을 찾는다. 설명된 분산의 50%까지 찾는 PCA 모델을 만들어 보자.
pca = PCA(n_components = 0.5)
pca.fit(fruits_2d)
print(pca.n_components_)
fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape)
scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
# output
# 2
# (300, 2)
# 0.993333
# 0.041221
차원이 축소된 데이터를 사용해 K - Means Clustering을 찾아보자.
km = KMeans(n_clusters = 3, random_state = 42)
km.fit(fruits_pca)
print(np.unique(km.labels_, return_counts = True))
for label in range(0, 3):
draw_fruits(fruits[km.labels_ == label])
print('\n')
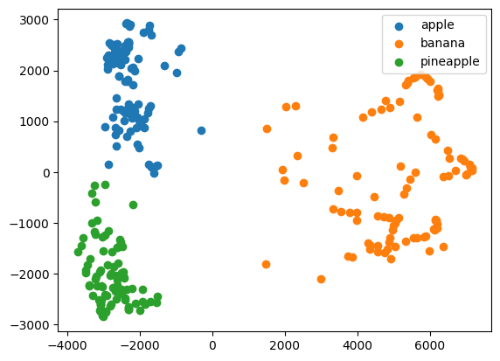
for label in range(0, 3):
data = fruits_pca[km.labels_ == label]
plt.scatter(data[:, 0], data[:, 1])
plt.legend(['apple', 'banana', 'pineapple'])
plt.show()
# output
# (array([0, 1, 2], dtype=int32), array([110, 99, 91]))
'혼공학습단' 카테고리의 다른 글
| [혼공머신] 6주차_인공 신경망 (0) | 2024.02.12 |
|---|---|
| [혼공머신] 4주차_트리 알고리즘과 앙상블 학습 (0) | 2024.01.29 |
| [혼공머신] 3주차(2)_확률적 경사 하강법 (0) | 2024.01.21 |
| [혼공머신] 3주차(1)_로지스틱 회귀 (0) | 2024.01.20 |
| [혼공머신] 2주차(2)_특성 공학과 규제 (0) | 2024.01.07 |



